Continuing with the optimization efforts of the ARM prover, this time I will explain an idea of @xuyang.
A major bottleneck that we are facing is the time to prove compliance of the ARM rules. Currently, the size of the compliance units (CUs) is fixed to 2: one consumed resource and one created resource. The main sources of inefficiency are:
- Many #CUs per action. Saying it differently, generation of many compliance proofs per action.
- Alignment overhead. Whether resources are created or consumed matters. It’s not the same an action with 4/4 resources, than an action with 7/1 resources. They both have 8 resources in total, but the former needs 4 CUs, and the latter needs 7 CUs.
Variable-size compliance units
The CU holds all the resources of the action:
pub struct ComplianceVarWitness {
/// The consumed resources.
pub consumed_resources: Vec<Resource>,
/// The created resources.
pub created_resources: Vec<Resource>,
/// The paths from the consumed commitments to the roots in the commitment trees
pub merkle_paths: Vec<MerklePath>,
/// The existing root for ephemeral resources
pub ephemeral_root: Digest,
/// Nullifier keys of the consumed resources
pub nf_keys: Vec<NullifierKey>,
/// Random scalar for delta commitment
pub rcv: Vec<u8>,
}
pub struct ComplianceVarInstance {
pub consumed_nullifiers: Vec<Digest>,
pub created_commitments: Vec<Digest>,
pub consumed_logic_refs: Vec<Digest>,
pub consumed_commitments_tree_roots: Vec<Digest>,
pub created_logic_refs: Vec<Digest>,
pub delta_x: [u32; 8],
pub delta_y: [u32; 8],
}
pub struct ComplianceVarUnit {
// vk is a constant in the compliance unit, so we don't place it here.
pub proof: Option<Vec<u8>>,
pub instance: Vec<u8>,
}
There will be just one ComplianceVarUnit per action. Which means, only one proof needs to be generated. This makes a difference, as the proving cost is amortized among all resources of the action. With the added benefit of removing padding resources and its overhead: it costs (roughly) the same proving compliance of n resources, independently of how many of them are created or consumed.
Nonces
The nonce should be unique. This is guaranteed by making it dependent on the action’s context where resources are created. The suggestion is to derive the i-th created nonce from all the consumed nullifiers:
created_resources[i].nonce = hash(i,consumed_nullifiers)
where hash is a collision-resistant hash function, and the index i is the position the created resource occupies in the CU (i.e. in the action).
Comparison
A proof of concept implementation can be found in this branch of the arm-risc0 repository. As a bonus, it also comes with an implementation of the sigmabus technique described here, that optimizes via removing EC arithmetic from the compliance circuit.
Key takeaways (TL;DR):
- There is a significant drop on proving times when using variable-size CUs.
- For large actions (with many resources), the sigmabus approach outperforms the vanilla variabe-size approach.
Disclaimer: The strange pikes in the timings are because benchmarks are not averaged. They correspond to a single run (it would be hard to average using Bonsai, anyways). They should serve only as intuition. You can try to reproduce the benchmarks running:
BONSAI_API_URL=https://api.bonsai.xyz/ BONSAI_API_KEY=XXX cargo test --release --features 'bonsai test' bench_compliance_2_var_sigmabus -- --no-capture
I have benchmarked using the Bonsai prover. I have not used a GPU.
2-size vs variable-size
For actions with just 2 resources, both approaches are essentially the same; which makes sense as in both case a single proof is generated. With 3 resources, the variable-size approach is ~2x faster, and with as little as 8 resources, it is ~5x faster. I stopped here due to the large proving times for the 2-size CUs, but the scaling factor should continue increasing with the number of resources per action. These timings confirm that the variable-size proving cost is amortized across all resources, and suggests that the more resources, the larger the amortization.
| circuit | resources (consumed,created) | proving time | #CUs | alignment overhead |
|---|---|---|---|---|
| 2-size | 2 (1,1) | 10.457182298s | 1 | |
| var | 2 (1, 1) | 11.430059181s | 1 | |
| 2-size | 3 (2, 1) | 26.866941109s | 2 | 6.716735277s |
| var | 3 (2, 1) | 15.357052552s | 1 | |
| 2-size | 4 (2, 2) | 25.885114226s | 2 | |
| var | 4 (2, 2) | 15.587812528s | 1 | |
| 2-size | 8 (4, 4) | 43.110295019s | 4 | |
| var | 8 (4, 4) | 15.82804433s | 1 | |
| 2-size | 8 (7, 1) | 73.768590046s | 7 | 31.615110018s |
| var | 8 (7, 1) | 15.560026139s | 1 |
variable-size vs sigmbabus
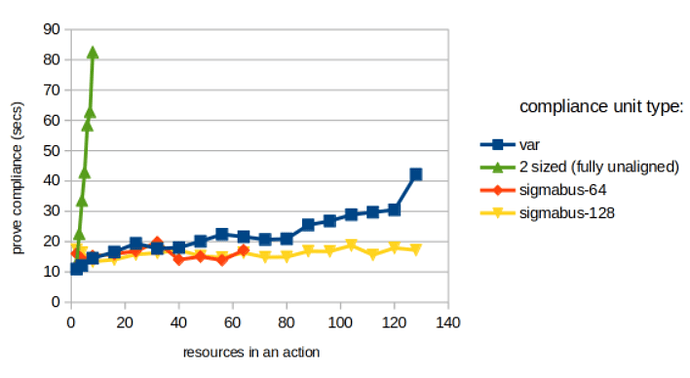
For actions with up to ~64 resources, their difference is not that much. In the extreme tested scenario (128 resources), variable-size takes ~40 seconds, whereas sigmabus takes ~17 seconds. In general, seems that the proving overhead increases faster for variable-size CUs – in the diagram below, the blue lines grows faster than the yellow line. Looks like sigmabus-128 stabilises at 20 secs.
Cap on resources. It’s worth noting that a sigmabus CU imposes an upper bound on the number of resources that can appear in a final (balanced) transaction. Benchmarks are for up to 64 and 128 resources per transaction. There doesn’t seem to be significant differences, which is good. It means we can settle for large upper bounds. (Yes, it is bad to have a cap on resources, but note there are other factors to consider, e.g. the current Ethereum controller seems to cap at ~100 resources per tx, due to gas limit constraints.)